Introdução
As Funções logarítmicas são as funções em que utilizam na sua lei de formação o operador logaritmo. Como o logaritmo é a operação inversa da exponencial, seus respectivos tipos de funções também são inversas uma da outra. Por este motivo as Funções logarítmicas são na maioria das vezes utilizadas nas mesmas áreas de aplicações. Portanto, neste trabalho irá abordar-se o tema que diz respeito a funções logarítmicas.
Função Logarítmica
Toda função definida pela lei de formação f(x) = logax, com a ≠ 1 e a > 0 é denominada função logarítmica de base a. Nesse tipo de função o domínio é representado pelo conjunto dos números reais maiores que zero e o contradomínio, o conjunto dos reais.
Exemplos de funções logarítmicas:
- f(x) = log2x
- f(x) = log3x
- f(x) = log1/2x
- f(x) = log10x
- f(x) = log1/3x
- f(x) = log4x
- f(x) = log2(x – 1)
- f(x) = log0,5x
Determinando o domínio da função logarítmica
Dada a função f(x) = log(x – 2) (4 – x), temos as seguintes restrições:
1) 4 – x > 0 → – x > – 4 → x < 4
2) x – 2 > 0 → x > 2
3) x – 2 ≠ 1 → x ≠ 1+2 → x ≠ 3
Realizando a intersecção das restrições 1, 2 e 3, temos o seguinte resultado: 2 < x < 3 e 3 < x < 4.
Dessa forma, D = {x ? R / 2 < x < 3 e 3 < x < 4}
Gráfico de uma função logarítmica
Para a construção do gráfico da função logarítmica devemos estar atentos a duas situações:
? a > 1
? 0 < a < 1
Para a > 1, temos o gráfico da seguinte forma:
Função crescente
Características do gráfico da função logarítmica y = logax
O gráfico está totalmente à direita do eixo y, pois ela é definida para x > 0.
Intersecta o eixo das abscissas no ponto (1,0), então a raiz da função é x = 1.
Note que y assume todos as soluções reais, por isso dizemos que a Im(imagem) = R.
Através dos estudos das funções logarítmicas, chegamos à conclusão de que ela é uma função inversa da exponencial.
Observe o gráfico comparativo a seguir:
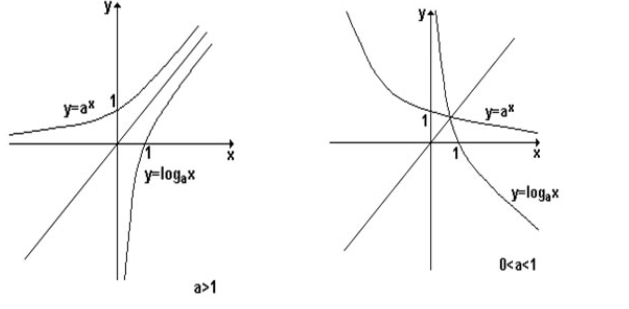
Podemos notar que (x,y) está no gráfico da função logarítmica se o seu inverso (y,x) está na função exponencial de mesma base.
Caso a função for multiplicada por uma constante b da forma, produzirá uma alongamento na função se b>1 ou se 0<b<1 a função será comprimida.
Caso b for uma valor negativo ocorrerá um espelhamento em relação ao eixo x, respeitando as mesmas regras dos valores positivos, ou seja, a função será alongada seb<-1 e comprimida se -1<b<0.
A função na sua forma básica intersecta o eixo das abscissas no ponto (1,0). Caso somarmos uma constante c no logaritmando, esta produzirá um deslocamento horizontal no gráfico.
Se c for positivo o gráfico será deslocado para esquerda e se for negativo será deslocado para a direita.
Exemplo 1:
A figura 1 abaixo sugere que se b > 0 e b 1, então o gráfico de y = satisfaz o teste da reta horizontal, e isso implica que a função f (x) = tem uma inversa.
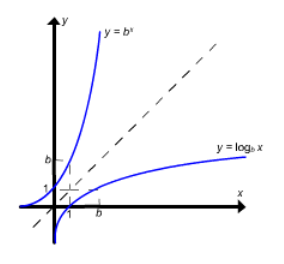
Exemplo 2:
As funções logarítmicas envolvem em sua resolução, propriedades destinadas ao estudo dos logaritmos. Portanto, o seu desenvolvimento depende do conhecimento prévio dessas propriedades.
Na equação: Q = Q0 * e– r * t, Q representa a massa final da substância, Q0, a massa inicial, r, a taxa de variação e t, o tempo em anos. Note que nessa equação, a massa final está em função do tempo t. Com base nessa equação, vamos determinar em quantos anos 50 g de uma substância se reduz a 5 g, obedecendo a uma taxa de variação de 8% ao ano.
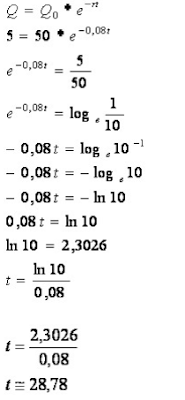
O tempo para que ocorra a redução é de aproximadamente 28 anos e 9 meses.
Conclusão
Caso a função for multiplicada por uma constante b da forma, produzirá uma alongamento na função se b>1 ou se 0<b<1 a função será comprimida.
Caso b for uma valor negativo ocorrerá um espelhamento em relação ao eixo x, respeitando as mesmas regras dos valores positivos, ou seja, a função será alongada seb<-1 e comprimida se -1<b<0.
Podemos representar graficamente uma função logarítmica da mesma forma que fizemos com a função exponencial, ou seja, escolhendo alguns valores para x e montando uma tabela com os respectivos valores de f(x). Depois localizamos os pontos no plano cartesiano e traçamos a curva do gráfico.
Bibliografia
- Lima, E.L.; et al. (2006). A matemática do ensino médio - vol. 1. [S.l.]: SBM
- Iezzi, G.; et al. (2013). Fundamentos de Matemática Elementar - Vol. 2 10 ed. [S.l.]: Atual.
- Stewart, James (2013). Cálculo - vol. 1 7 ed. [S.l.]: Cengage.
- Anton, H.; et al. (2014). Cálculo - Volume I 10 ed. [S.l.]: Bookman